Экономическим прогнозированием я стал заниматься ещё со студенческих лет. Моя кандидатская диссертация была посвящена прогнозированию спроса на электроэнергию со стороны промышленности, а докторская — анализу и прогнозированию экономической конъюнктуры.

Есть по этому поводу многочисленные статьи и монографии, но наиболее полно результаты моих исследований изложены в двухтомном учебнике, который мы с Иваном С. Светуньковым опубликовали в издательстве «Юрайт»:

1. Светуньков И.С., Светуньков С.Г. Методы и модели социально-экономического прогнозирования: учебник и практикум для академического бакалавриата. В 2-х т. Т. 1. Теория и методология прогнозирования. М.: Издательство Юрайт, 2014, 2015, 2016, 2017, 2018, 2019. 351 с.
2. Светуньков И.С., Светуньков С.Г. Методы и модели социально-экономического прогнозирования: учебник и практикум для академического бакалавриата. В 2-х т. Т. 2. Модели и методы. М.: Издательство Юрайт, 2014, 2015, 2016, 2017, 2018, 2019.  450 с.

Вообще-то по просьбе издательства мы рукопись сократили, иначе получился бы трёхтомник, а такие учебники, по мнению издательства, не продаются.

Здесь я расскажу о том, что принципиально нового я привнёс в теорию прогнозирования.

1. Классификация динамических процессов

Прежде всего, я навёл порядок с пониманием того, что такое в экономическим прогнозировании «временной ряд» (динамический ряд). Подавляющее большинство прогнозистов считает, что временной ряд — это просто упорядоченный во времени ряд каких-то значений. Но в экономике это не так. Вот пример: показатель численности населения в СССР в 1937 году. Мы же понимаем, что год 1937 является не просто индексом упорядочивания. Он характеризует состояние политической, международной, социальной, экономической и военной конъюнктуры того времени. И мы понимаем, что время в этом примере является характеристикой этого состояния, а не номером наблюдения.

Временным (динамическим) можно назвать упорядоченный во времени ряд наблюдений, в котором время наблюдения характеризует особенность состояния внешних и внутренних факторов поведения объекта наблюдения, в результате чего формирование ряда осуществляется неслучайным образом.

Тогда и для обработки такого ряда для прогнозирования следует использовать другие методы, нежели для обработки упорядоченного во времени ряда случайных значений. Для того, чтобы окончательно понять, в чём особенности именно экономического прогнозирования временных рядов, я предложил такую классификацию экономических процессов [1]:

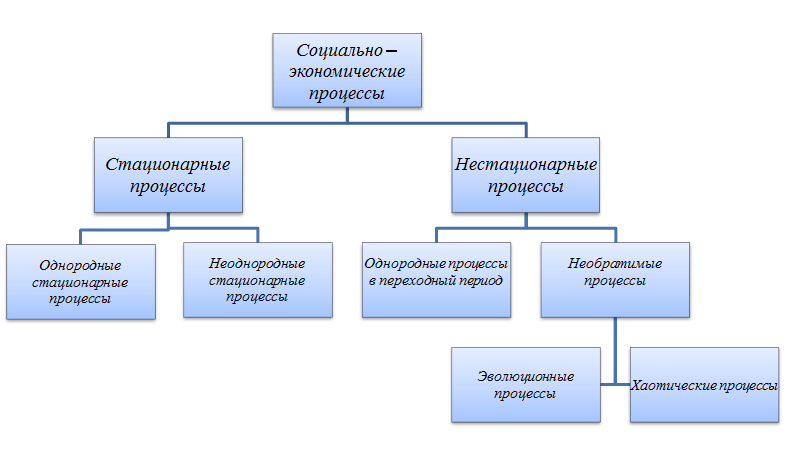
Временнóй ряд может формироваться в разных условиях, которые предопределяют его характеристики и свойства. В наиболее общем случае он может отражать два типа процессов — обратимые и необратимые.  

Обратимые процессы представляют собой такой тип развития объекта, который характеризуется постоянством качественных характеристик при изменении его количественных показателей как результат реакции на изменение внешних условий. Если внешние условия остаются стабильными, изменение количественных характеристик обратимого процесса определяется только действием случайных факторов ε.

Из этого понимания обратимого процесса следует, что если в ходе его развития внешние условия x_t станут такими же, как прежде (x_t = x₀), то количественные характеристики процесса y_t вернутся к прежним величинам (y_t = y₀), искажаемым разве что влиянием случайных факторов y₀ + ε.

Под необратимым процессом будем понимать такой тип развития объекта, который характеризуется изменением во времени его количественных характеристик, а также структуры элементов, степени и направления взаимосвязей между ними. Это означает, что если внешние условия протекания процесса остаются стабильными, в нем все равно продолжают происходить изменения, вызванные внутренними факторами и силами, постепенно меняющими структуру процесса.

Процесс претерпевает во времени необратимые изменения, поэтому, если в ходе его развития внешние условия x_t станут такими же, как прежде (x_t = x₀), то количественные характеристики процесса y_t будут существенно отличаться от прежней величины (y_t  ≠ y₀).

Обратимые процессы могут иметь самую разную природу и самый разный вид, но и эту сложную совокупность можно разделить на две группы: 1)стационарные и 2)нестационарные обратимые процессы.

Под стационарными рядами понимаются ряды случайных процессов, характеристики которых не меняются с течением времени t, т.е. они инвариантны относительно временных сдвигов.

Характеристики этих процессов (математическое ожидание, дисперсия и пр.) могут быть найдены с заданной степенью точности, в результате чего задача прогнозирования таких стационарных процессов становится чрезвычайно простой. В то же время стационарные процессы могут иметь самый различный характер динамики — изменение одной их части не имеет ярко выраженных тенденций, динамика другой — имеет явно выраженную тенденцию изменения, которая может носить и очень сложный нелинейный характер.

Поэтому стационарная группа типов динамики временнóго ряда может быть в свою очередь разделена на две подгруппы:

•  однородный обратимый процесс;

•  неоднородный обратимый процесс.

Однородные стационарные процессы прогнозируются с помощью методов математической статистики.

Чаще всего можно утверждать наличие закона нормального распределения и поэтому основные усилия должны быть направлены на доказательство данного положения с помощью соответствующих статистических гипотез и методов их проверки, а после этого — на вычисление характеристик процесса.

В этом случае лучшей оценкой его математического ожидания выступает средняя арифметическая, а лучшей оценкой дисперсии — выборочная дисперсия.

Здесь уместен основной принцип выборочного метода — чем больше наблюдений, тем лучше оценки модели.

Неоднородные стационарные процессы свидетельствуют о наличии множества факторов, меняющих свои количественные характеристики и воздействующих на объект, показатели которого в ответ на это воздействие меняются во времени.

Поэтому задачей прогнозиста является выявление факторов, влияющих на процесс и построение модели, описывающей их количественное влияние на объект прогнозирования.

И в этом случае оценки прогнозных моделей с увеличением числа наблюдений улучшаются.

Нестационарные обратимые процессы, в противоположность стационарным, характеризуются такими изменениями их основных характеристик, которые не вытекают из прежних значений. Под нестационарными в промежуток времени от t до t + T обратимыми процессами понимаются такие из них, характеристики которых меняются вариантно относительно временных сдвигов.

В математической статистике нестационарные процессы рассматривают как переход стационарного процесса от одного уровня к другому.

Нестационарность случайного процесса происходить «за счёт переменного математического ожидания» — тогда следует определить форму этого математического ожидания и вычесть его от уровней ряда.

Довольно часто этот переход характеризуется постоянством первой или второй производной. Поэтому для прогнозирования таких нестационарных процессов используют различные процедуры приведения к стационарности – прогнозируют первые или вторые разности, или, обнаружив явление автокорреляции, устраняют её.

Ситуация значительно усложняется, когда нестационарный процесс протекает в условиях неоднородности.

Факторы внешней среды при этом претерпевают значительные изменения, что оказывает влияние на объект прогнозирования и его поведение, причём эти изменения не вытекают ни из свойств самого процесса, ни из состояния внешней среды.

Сам объект, адаптируясь к этим внешним изменениям, меняет свои характеристики — качественные и количественные.

Наступают необратимые изменения в процессе, которые отражены в ряде динамики его показателей.

В зависимости от того, насколько меняются во времени приращения ∆y(τ), такие необратимые процессы могут быть выделены в две подгруппы:

1) хаотические и

2) эволюционные процессы.

В случае, когда приращения ∆y(τ) не имеют какой-либо достаточно гладкой тенденции во времени и их изменения хаотичны (например, на первом же наблюдении ∆y(1) может быть достаточно велико в сравнении с самим показателем y(1)), такие процессы могут быть отнесены к хаотическим. Отношение ∆y(t + τ) / y(t + τ) непредсказуемо в любой момент времени — по модулю оно может быть очень большим либо близиться к нулю.

Если приращения ∆y(τ) постепенно нарастают с течением времени т в результате количественных и качественных изменений, происходящих в объекте, чей реализацией является нестационарный ряд, то эти процессы могут быть названы эволюционными. При этом отношение ∆y(t+τ) / y(t+τ), харак­теризующее нарастание неопределённости, имеет увеличивающуюся со временем т динамику — от нуля до бесконечности.

Теперь ясно, что в экономическом прогнозировании следует использовать три методологически разные группы методов прогнозирования:

1. Методы регрессионно-корреляционного анализа (для обратимых процессов, для однородных процессов в переходный период, называемых нестационарными),
2. Методы теории хаоса и теории ошибок (для хаотических процессов),
3. Адаптивные методы прогнозирования (для эволюционных процессов).

2. Запредельное множество экспоненциального сглаживания (метода Брауна)

Самый популярный метод экономического прогнозирования — метод экспоненциального сглаживания, который у нас в России любят называть по имени его автора — «метод Брауна». Ошибочно считается, что постоянная сглаживания в этом методе меняется от нуля до единицы. Я показал ещё в 90-е годы прошлого века, что пределы её изменения значительно шире — от нуля до двух (Светуньков С.Г. Запредельные случаи метода Брауна // Экономические науки: Ученые записки УлГУ. Ульяновск: Изд-во СВНЦ,1997.  Вып.2. Часть 1 ).

Дальнейшие мои исследования в этом направлении, в том числе проведённые вместе с моими коллегами, показали, что для прогнозирования стационарных процессов лучшими являются модели экспоненциального сглаживания с постоянной сглаживания, лежащей в классических пределах (от нуля до единицы), а для прогнозирования нестационарных процессов — лежащей в запредельном множестве (от единицы до двух). Недавно я с удивлением встретил научные публикации, в которых это множество от единицы до двух называют «множество Светунькова». Не я это название придумал…

В экономике России протекают в основном нестационарные процессы и в 70% случаях постоянная сглаживания должна лежать в пределах от единицы до нуля. Так что использование запредельного множества метода экспоненциального сглаживания очень важно для более точного экономического прогнозирования в России. Кстати, в MS Excel заложен суженный классический интервал — от нуля до единицы.

3. Метод неравномерного сглаживания

В его основе лежит метод стохастической аппроксимации.

Будет время — опишу более подробно…